コンピュータグラフィックス特論 課題(2011年度)
下記のプログラミング課題において4問中少なくとも3問を提出せよ。
プログラミング課題
インタラクティブ性のあるプログラムが理想であり、
それを遠隔地でも評価するにはJavaで作成すると効果的であるので、可能な人はできるだけJavaを試みて下さい(この場合画像サイズは300x300以下でもよい)。
C言語とOpenGLを用いて表示する方法でもよい。
この際、出力例がカラー画像の場合、それを評価して欲しい人は、自分のホームページに画像を置いて見れるようにしてもよい。
課題 1 Bezier曲線の描画プログラムを作成せよ。
- n次の曲線を描画する下記の3方法でのプログラムを作成せよ。
- 方法A;パラメターをtとし、tをΔt(例えば0.05)ごと増分し、パラメターtの際の曲線上の点(x(t), y(t))をBezier曲線の定義式で計算し、それらの点列をプロットする。
- 方法B; Bezier曲線の定義式ではなく、曲線をDeCastejouの方法を利用して、パラメータtで2分割してえられる際の制御点が曲線上の点になるので、それらの点列をプロットする(講義中の配布資料参考)。
- 方法C;次数を1つ上げた場合の制御点をプロってしてみる。次数を繰り返してあげれば、制御点は曲線に近づくのを利用する。すなわち制御点をプロットすれば曲線となる
- 次のURLのアプレットを参照せよ。 /~nis/javaexampl/bezie.htm
- 有理Bezier曲線も描けるようにし、真円(3または4個の曲線で表現)を描くプログラムを作成せよ。
課題 2 n次のBezier曲線と線分の交点を求めるプログラムを作成せよ
- 制御点(たとえば4点)を含む凸包(制御点を囲む最小の凸多角形)を求めて描画せよ。
- 曲線と直線(任意の2点で指定)との交差は、凸包と直線が交差しなければ、曲線との交点はない性質を利用して、交点を曲線分割で抽出せよ。曲線を2分割して、それらの凸包から交差の可能性をチエックする方法で、交差の可能性のある区間を狭めていく方法を利用する。(なお、線分がx軸になるように制御点を回転してから処理すると交差判定が容易である。)
- 余裕があれば(必修ではない)、より効率のいいBezier Clipping法で交点を計算せよ
課題 3 フラクタル(自己相似性)の考え方を用いて、線画によって自然物を描画するプログラムを2つ以上作成せよ 。
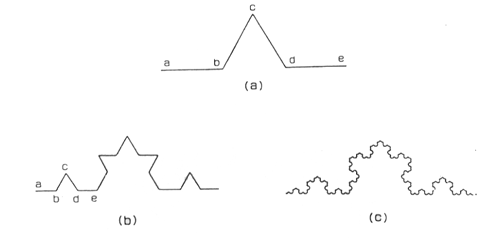
- 海岸線、雲や煙、雷の形状、植物などの形は、全体の形と部分の形がよく似ているという特徴がある。このような特徴をもつ図形をフラクタルという。
- 代表的な自然物のフラクタル図形には以下の例がある。下にそれぞれの画像をあわせて示す。
雪の結晶(コッホ曲線の利用)
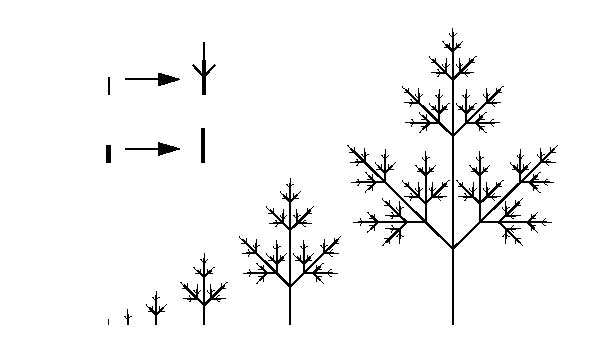
樹木
山脈(参考リンク:http://en.wikipedia.org/wiki/File:Animated_fractal_mountain.gif )
オウムガイ
この例示以外にもフラクタルの考え方を用いて作成した自然物をプログラミングにより作成しているものであれば良い。
ただし、自然物として何を表現したかを明記すること。
- プログラミング時には再帰関数を利用すること。
- 【任意】 静止画を表示するだけでなく、ユーザーのパラメータの調整によってさまざまな画像を生成できるようプログラムを改良すること。
|
|
図3.1 コッホ曲線による雪の結晶 |
図3.2 フラクタルによる樹木の表現 |
|
|
図3.3 フラクタルによる山脈作成のアニメーション |
図3.4 オウムガイに見られるフラクタル図形 |
課題4 マウスドラッグによって色鉛筆風のストローク生成ができる簡易ペイントツールを作成せよ。
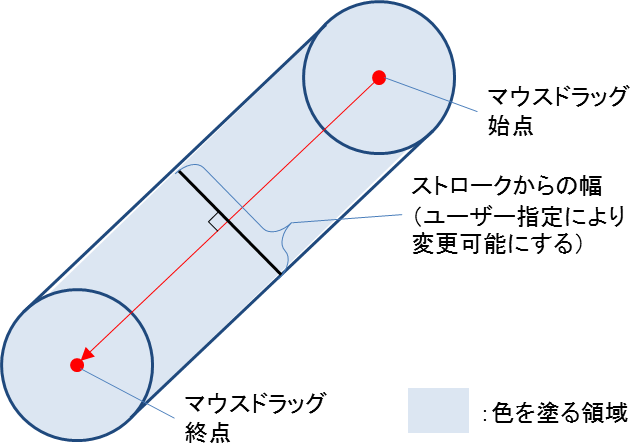
- マウスドラッグによって得られる線(ストローク)から一定以上の距離までを色を塗る領域とする。(ペンの太さに関係する 図4.1参照)
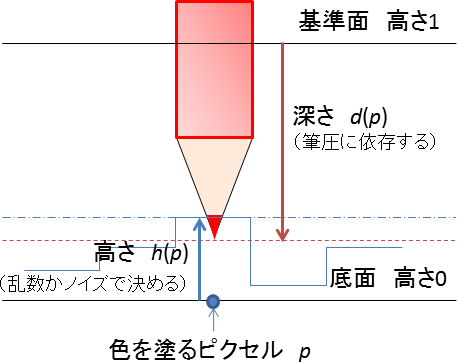
- ストロークを描くキャンバスは紙質による凹凸を乱数またはノイズ関数によって再現し、ペンからの高さに応じて確率的に色を分配する。
(ペンの筆圧に関係する 図4.2参照)
- 重ね塗り可能にし、複数回ストローク(それによる色塗り領域)を重ねることで使用した色に近付くようなモデルにすること。
参考文献[3]の3節 Stroke Modelを参照すると良い。
- ペンは太さ、筆圧、色をいくつか選択可能であるようにすること。
- 【任意】 結果画像を保存する機能など、実際のペイントツールと同じような機能があるとなお良い。
|
|
図4.1 ストロークと色を塗る領域の関係 |
図4.2 紙質と筆圧の表現 |
参考文献
[1] 「コンピュータグラフィックス」、 CGARTS(画像情報教育振興協会)
[2] /~nis/CG/cgtxt/cg2/cg026.htm#cg26
[3] Creating Colored Pencil Style Images by Drawing Strokes Based on Boundaries of Regions
参照URL
Webでの本課題公開 : (訂正がある場合があるので、提出前に再度下記を見ること)
/~nis/junk/lecture/VisRep11.html
本講義のサイト
/~nis/junk/cg_lectur.html
注:プログラミングが困難な学生は,下記のレポート課題を提出しても構いません。
課題1
3次元の座標変換に関し、x軸に関して30度回転した後、y軸に関して45度回転する変換マトリックスを求めよ。また、、y軸に関して45度回転した後、x軸に関して30度回転する変換マトリックスを求めよ。これらの2つの変換マトリックスは同じかどうか議論せよ。
課題2
直線Lとn次Bezier曲線との距離はn次Bzier曲線となることを示せ。また、Bezier曲線の各頂点への基底関数は合計すると常に1になることを示せ。
課題3
代表的な隠面消去の方法を3つ以上挙げ、その基本的な方法と特徴をのべよ(取り上げた方法の比較も含む)。
課題4
単純な例(球が1つの場合)でのレートレーシングに関して計算法を記述せよ。球の中心をPc、半径をr、視点の位置をPv、視線の方向をベクトルVとすると、レイと球の交点Qを求める式を抽出し、その交点Qでの反射方向ベクトルRと屈折方向ベクトルTの算出式を書け。
課題5
下記の中から有用なCGの要素技術を2つを選びその技術内容を述べよ(可能なら開発者名も、計1ページ以上とする)。
フラクタル、NURBS,ボリュームレンダリング、Bスプライン曲線、ラジオシテイ法、バンプマッピング、マンデルブロー集合、サブサーフェススキャタリング、イメージベースレンダリング、レイキャスティング
締切: 2月16日(木曜)23:00!
結果(プログラムソース、実行形式、結果画像、レポート)は各自のホームページに置くか、メイルに添付して下さい。メイルの際はTAの石川 ishi@nis-lab.is.s.u-tokyo.ac.jp にもccして下さい。
連絡先:email: nis@is.s.u-tokyo.ac.jp
電話: 03-5841-4106 (西田研究室):
/~nis/
注: 2月16日(課題締切日ですが課題にプラスになる)講演会(テキサス大のBajaj教授)に参加し,その内容要旨および感想をA4程度で書いて提出すると配慮します。