  
|
  
|
|
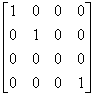
3次元物体を2次元で表現するには投影が必要である。投影法としては、平行投影と透視投影がある。他に、斜投影、軸測投影があるが省略する。(文献3参照)。 平行投影の中で簡単なものに正投影がある。x-y平面(他のy-z、z-x平面でも同様)を投影面とすると、正投影はz座標を0とすることにより簡単に得られる。すなわち、変換行列は、
 (2.13) (2.13)3次元物体を眺めた場合、図1.1のように、近くが大きく、遠方が小さく見える。こうした効果を表現できる投影法を透視投影(perspective projection)という。
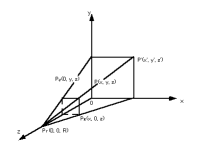
簡単のため、投影面がx-y平面で、投影中心(視点に相当)がz軸上(原点から距離R)にある場合の、点P(x, y, z)の透視投影について説明する。図2.6のように、点Pが投影面に投影されたときの点をP'(x', y', z')とすると、三角形の相似から、次式が得られる。
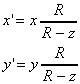 (2.14) (2.14)これを同次座標で表現すると、次式で表される。
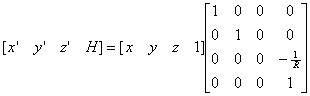 (2.15) (2.15)
上式から
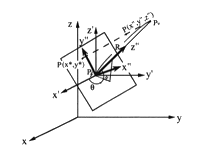
図2.7:透視変換 この変換は、まず (a) 注視点を原点とするように平行移動し、 (b) 視線(注視点と視点を結ぶ直線)が、投影面に垂直になるように回転する。 (c) 最後に投影面への透視投影をする。 前述の4×4の変換行列で表現するのが理想であるが、その場合演算数が多くなるので、ここでは、通常のマトリクスで表現する、移動と回転を組み合わせた式は、
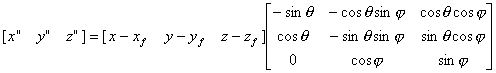 (2.16) (2.16)
となる。投影面での座標系での投影された点Pを(
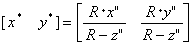 (2.17) (2.17)となる。ここで分母の(R-z'')は視点からの奥行きに相当する。 図2.8: 透視図形 | |
 前のページへ 前のページへ
| 次のページへ
|