インタラクテイブ性のあるプログラムが理想であり、それを遠隔地でも評価するにはJavaで作成すると効果的であるので、可能な人はできるだけJavaを試みなさい(この場合画像サイズは300x300以下でもよい)。
X-WindowあるいはOpenGLを用いてスクリーン上に表示する方法でもよい。この際、出力例がカラー画像の場合、それを評価して欲しい人は自分のホ
ームページに画像を置いて見れるようにしても良い。
課題1 中点変位法を利用して、ブラウン運動を軌跡を描画せよ。
- 直線からはじめて、中点変位法を利用して曲線を生成し、表示すること(資料[1]参照)。
- いくつかの複雑さのレベルを変えたものを描画すること。
- 4x4の格子点から始め、フラクタルにより複雑なフラクタルの山を生成せよ。
/~nis/javaexampl/zbuf/ZbufFract.html
- 上の地形はハイトフイールドといえる。等高さ曲線を描画することで通常の地図のように等高線を描画せよ(資料[1]参照)。
- 高さは、最高値と最低値を10等分して等高線を書くこと。
- 密度関数をいくつか配置し、その等高線を描画せよ。あるいは、ある閾値を設定し、その値より大きな部分を塗りつぶす方法で、何か図形を作成せよ(下記参照)。
/~nis/javaexampl/metcrc/metacrc.html
- Perlinノイズと呼ばれる連続的に変化を出力する関数を用いることによって、様々なパターンのテクスチャを作成することができる。
- Perlinノイズは、大理石のパターン(Marble)もよく用いられるものである。また、ガス状のパターンはスケールの異なるPerlinノイズの重ね合わせによって作られる(資料[2]参照)。
- Perlin氏のWEBページを参照してください(ノイズ関数のソースコード、適応例が紹介されてる)。
http://mrl.nyu.edu/~perlin/doc/oscar.html - Noise(オリジナルPerlinノイズ)、Turbulence、Marbleのアプレットは下記を参照のこと
/~nis/javaexampl/newJava/Perin/Perin.html
http://graphics.lcs.mit.edu/~legakis/MarbleApplet/marbleapplet.html
- まずプログレッシブ法で実験し、下図のようなL字形の部屋を例に表示し、
壁(完全拡散面)による光の遮蔽効果を考慮して考えること(資料[3]参照)。なお、底面(図のAB間)での分布のグラフを描画せよ。
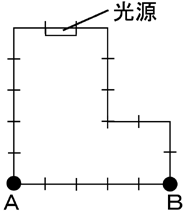
- 2次元の場合、下記のフォームファクタの定義式における分母の距離は2乗ではなく1次となる。

- 同じ形状の場合をモンテカルロ法でも行い比較せよ(資料[4]参照)。