課題
下記のプログラミング課題3問(選択)を提出して下さい。
プログラミング課題
インタラクテイブ性のあるプログラムが理想であり、それを遠隔地でも評価するにはJavaで作成すると効果的であるの
で、可能な人はできるだけJavaを試みて下さい(この場合画像サイズは300x300以下でもよい)。 OpenGLあるいはX-Windowを用い
てスクリーン上に表示する方法でもよい。この際、出力例がカラー画像の場合、それを評価して欲しい人は、自分のホ
ームページに画像を置いて見れるようにしても良い。
課題1. Kochのsnowflakeを描画するプログラムを作成せよ。
- 配布資料[1]の図9.3を参考に描画する。
- プログラムは再帰呼び出しの形式になるが、再帰呼び出しについては配布資料[2]のシルビンスキーのガスケットを参考にしてください。
課題2. 凸多角形の走査変換のプログラムを作成せよ。
- 走査線は下から上に移動するものとし、走査線と多角形の交点は増分法を用いて演算量が少なく算出せよ。
- 各頂点の色は異なることを許すものとし、多角形内はグローのスムーズシェーディングを用いて色を補間せよ。
課題3. 多角形のみで構成される面を考え、これらをBSPを使い効率よく隠面消去するプログラムを作成せよ。
- 多角形は2次元平面状にしていされた直線を垂直方向にスイープしたものとする。したがってBSPは2次元として処理できる。
- BSPについては配布資料[3]を参照のこと。
- 任意の視点位置が与えられると、3次元の多角形の頂点を透視投影が必要であるが、これは資料[2]のp.6を参照すること。
- 投影された多角形を視点から遠い順に塗りつぶすが、面の描画は課題2を利用する。
課題4 ラジオシティ法についてテストプログラムを作成せよ。
- 2次元の場合でプログラミングすればよい。図(a)のような簡単な室内をいくつかに分割して、各エレメント間のフォームファクタを計算し、それを用いてエネルギの授受を計算し、室内の光の分布を求めよ。
- 2次元の場合、下記のフォームファクタの定義式における分母の距離は2乗ではなく、1次となる。
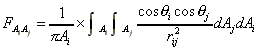
- 解法としてガウスザイデル法を始め色々な方法があるので、各自が効率のよいと思う方法で解け。
たとえば、プログレッシブリファインメント法(資料[4]参照)を利用してもよい。なお、ガウスザイデル法等の比較を加えてもよい。
- 障害物(図のように線分で表現してよい)を挿入し、その影響を調べる。各面での光の分布は、図(b)のようにグラフで表示してもよい。
- 各面の反射率は任意に与えて下さい。天井、壁、床、窓の各々の反射率を入力できるようにする。また各面の分割数(あるいは幅)も指定できるものとし、分割数による精度について比較検討できるとよい。
- 鏡面反射成分を効慮すると複雑になるので、拡散反射のみでよい。
- 光源は点光源とするか、分割した1つのエレメントを発光面とみなしてもよい。

注: 3問中1問は自由課題に置き換えてもよいが、その場合ある程度完成度の高いものとする。
あるいは、プログラミングが困難な学生は相談に応じてレポート課題を提出すること。
レポート課題
隠面消去の方法を分類し、それらの特徴を述べよ。
資料[5]を読んで、リアルな画像をえるための技術をまとめよ。
n次のBezier曲線とm次のBezier曲線を乗じるとBezier曲線になることを証明せよ。また、何次の曲線になるか?
直線Lとn次Bezier曲線との距離はn次Bzier曲線となることを示せ。
参考