Bezier Clipping
| < to my homepage | Publication list | SampleImages| Animation| CG Links| Research topics(in Japanese) > |
このページのスライド画像はクリックすると拡大画像が表示されます。 (2014/1１ 作成）
| OutLine
|
|
| 西田は1970年来,40年間ものCG研究を行っており、研究分
野(右
図参照）はかなり
広いがそのなかでもRenderingl関係で特にBezier Clippingに関する研究を紹介する。 この方法は、私が米国ＢＹＵに滞在中(1989)にＴ．Ｗ．Sederbergとの共同で開発した手法です . 最初は曲面のレイトレーシング法としてSIGGRAPH 1990で発表しましたが、広く応用する論文を多数発表した。曲線（や曲面）の交差判定に有効ばかりでなく、高次多項式の解を求めるのにも有効な方法であ る。 < Radiosity | Soft shadow | Bezier Clipping | Light Scattering | Natural phenomena > |
 研究分野 |
|
|
  Ｂｅｚｉｅｒ Clippingは上のように多くの応用があります。  |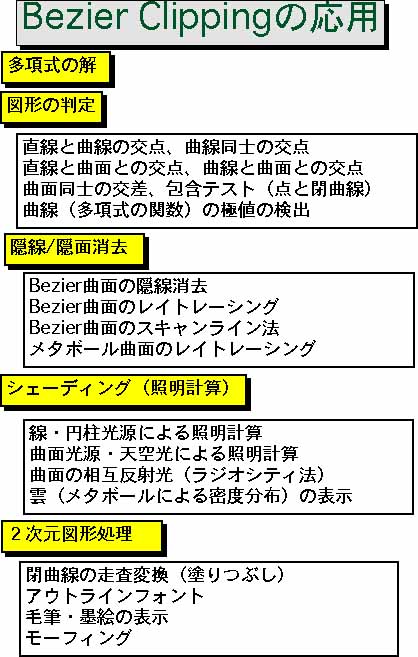
Bezier Clippingを紹介してる書籍・Hoschk, Lasser, "Fundamentals of Computer Aided Geometric Design", AK Peters, (1989)・鳥谷、千代倉、「３次元ＣＡＤの基礎と応用」共立出版(1991): ・ G.Farin, "Curves and Surfaces for CAGD" 4th Ed.,Academic Press (1996) ・T.Akenine-Noller, E.Haines,"Real-time Renderin", AK Peters (2002) ・G.Farin, "Handbook of Computer Aided Geometric Design," North-Holland, Elsevier 2002 ・T.A.-Moller,etc., "Real-Time Rendering", A.K.Petters, 2008 Bezier Clippingを紹介してるサイト・ Bezier clipping - ウィキペディア・ 直 線との交点(Bezier Clipping) | ProgrammingCity・ 交 点 | ProgrammingCity・ Bezier clipping・ Bezier Clippingの解説（旧版）・Bezier Clippingの英文解説（ｐｄｆ）  |
|
|
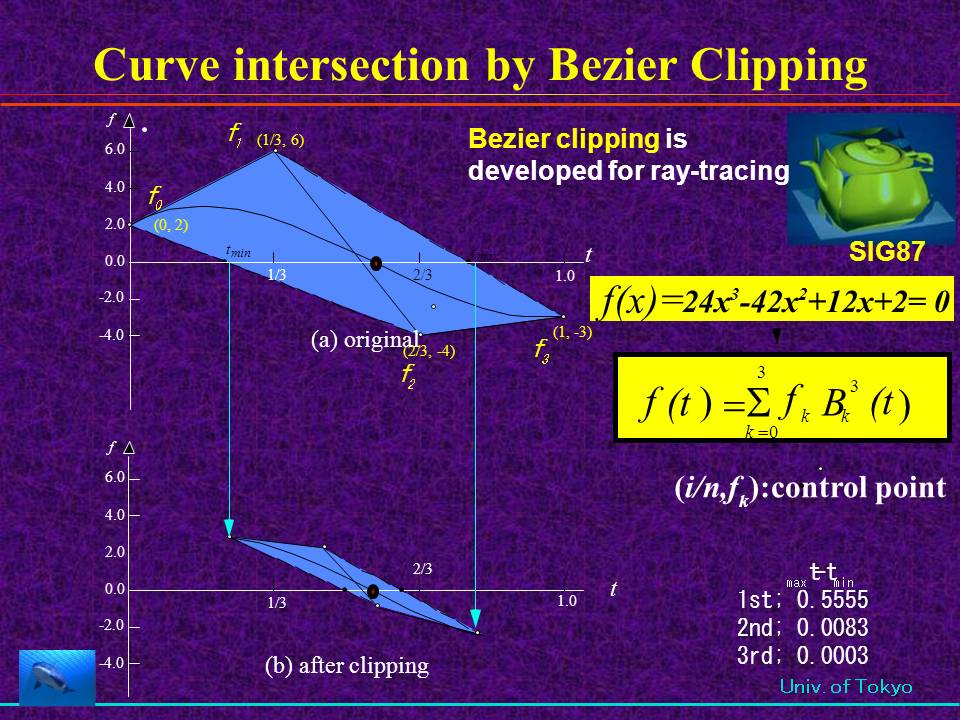 多項式は必ずＢｅｚｉｅｒ曲線(関数）に変換できます(上のは3次式の例）。Ｂｅｚｉｅｒ関数の解は必ず、その関数の制御多角形と軸との交差区間に存在し ます。 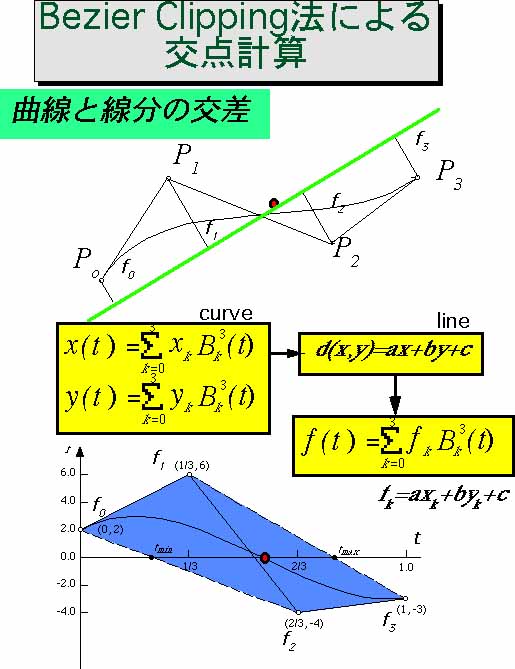 直線とbezier曲線との距離はBezier関数となる。この関数が０になる点が交点である。 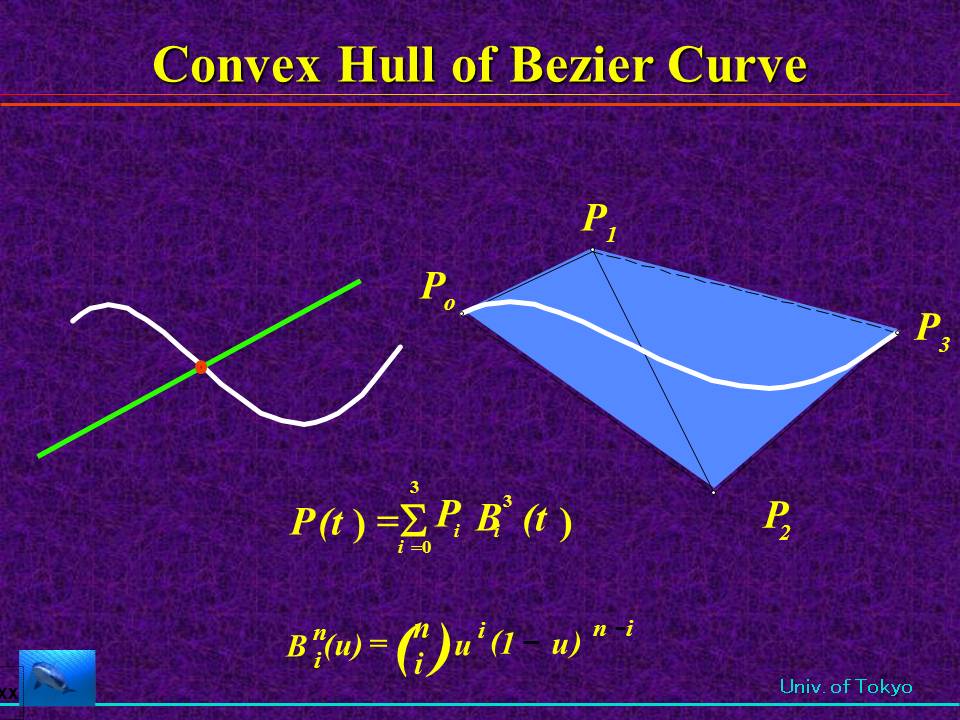 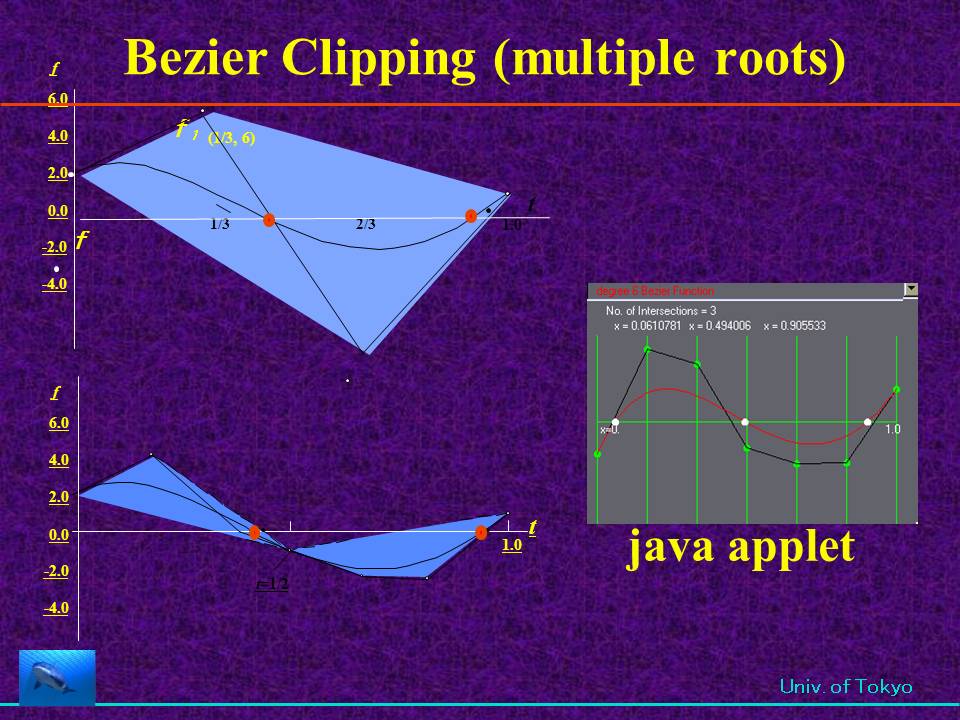 多項式の解（交点）が複数ある場合も求められます。収束が遅い場合関数を2分割し、それぞれにclippingを適用すれば、複数解でも収束します。 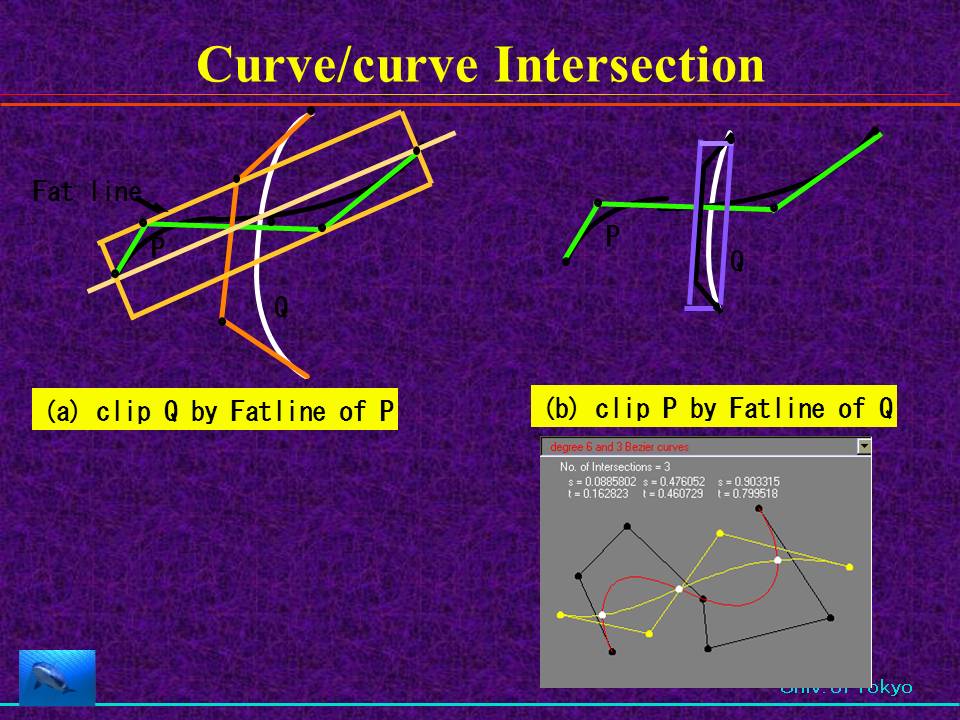 曲線同志の交差判定もできます。これには曲線の凸包を含む幅のある線（ＦＡＴ ＬＩＮＥと称す）で相手の曲線をクリップし、交互に適用すると両社の曲線の 幅は狭くなり、かつ短くない、最終的には直線同志の交差と等価になります。 |
 ＣＧの歴史上重要な技術の開発と受賞者(SIGGRAPH S.A.Coons賞など）との関係  共同開発者のSederberg 著者らのＢｅｚｉｅｒＣｌｉｐｐｉｎｇ関連論文； "Ray
tracing
trimmed rational surface patches" by T Nishita, TW Sederberg, M
Kakimoto - ACM SIGGRAPH Computer Graphics, 1990
"Curve
intersection usingBezier clipping"
by
TW Sederberg, T Nishita - Computer-Aided Design, 1990 - Elsevier
|
|
|
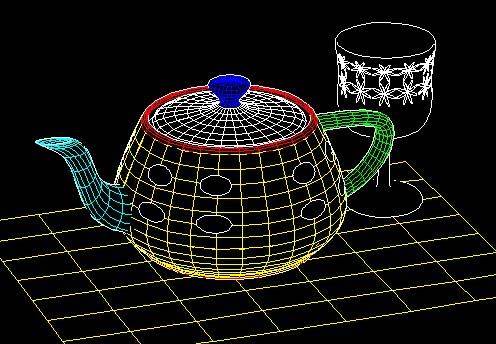
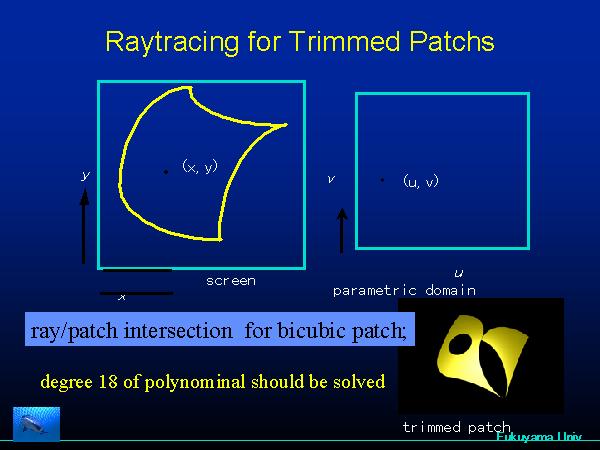 Ｂｅｚｉｅｒ ClippingはTrimmed Ｂｅｚｅｉｒ曲面を対象にしたレイトレーシング法として開発したものである。Trimmed Ｂｅｚｅｉｒ曲面とは、 曲面に穴が開いているものを示す(上図の下参照）。曲面のレイトレーシングとは、スクリーンに投影された曲面において、スクリーン座標（ｘ、ｙ）を指定す ると、それに対応する曲面に曲面座標（u,v)を算出する問題である。普通は(u,v)を与えると、それに対応する（Ｘ，Ｙ，Ｚ）座標が求まり、それをス クリーンに投影したものが(x,y)である。それに対してスクルーンの座標から、（u,v)を算出する逆問題であり、その計算は難易度の高い。 Kajiyaやこの問題に挑戦した。彼によると双3次曲面の場合368次式を解く必要がある。これは1次式の繰り返しのみで解けるようにしたのが、 Bezier Clippingである。 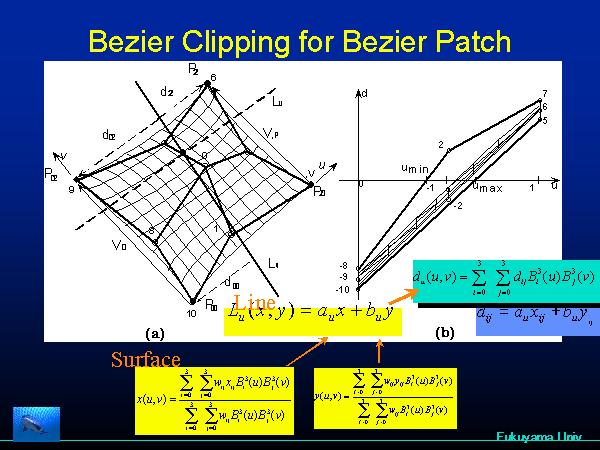 スクリーン上の点(x,y)から曲面座標(u,v)を算出する問題を考える。(x,y)を通過する2本の直線を考える。この直線からの制御点の距離(1次 式で計算できる）をuに関する関数としてプロットしたのが右図である。これらの凸包の中に必ず解は存在する。同じようにｖにおいても求められる。解は必ず u軸と凸包の交差区間に存在するから。この区間で曲面を再分割する。するとこの曲面は小さくなり平面に近づく。v成分についても同じ操作をする。 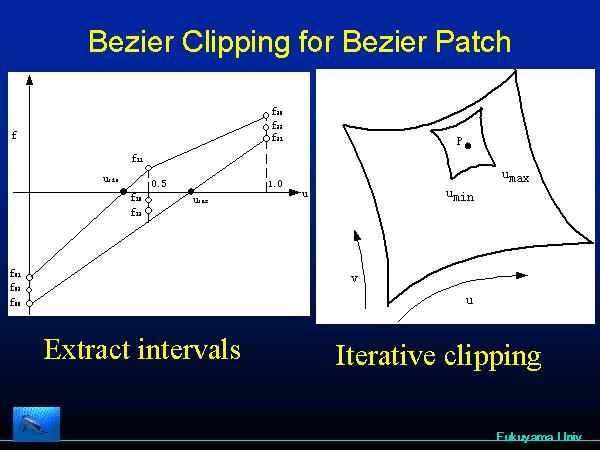 上の左図はuの存在区間[umin, umax]を求めており。ｖ成分も同様に求め、右図はその区間で曲面を分割したものである。わずか3回の分割でほぼ点になる。このときの(u,v)が解で あ る。  SIGGRAPH 1990：Ｓｅｄｅｒｂｅｒｇの提唱したＦＦＤ法により曲面を自由変形し、その後にレイトレーショング法で描画   ＣＧ界では良く使用される、ユタのティーポットはBezier 曲面で構成されており、この曲面をレイトレーシング法で表示した例。 |
|
|
|
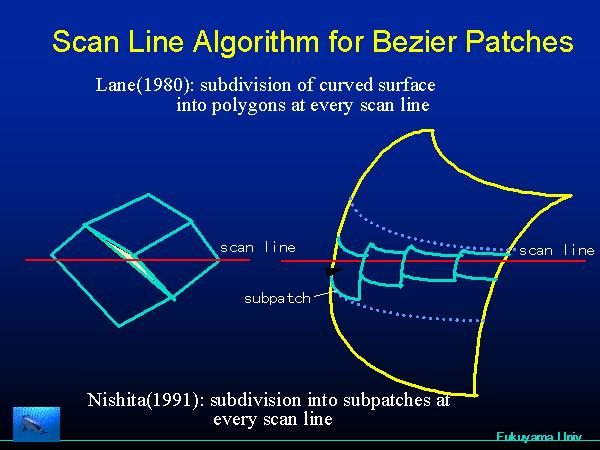  Ｓｃａｎ Ｌｉｎｅ法は、走査線を動かし、走査線単位で可視領域を抽出する方法である(1991年）。走査線と重なるいくつかのサブパッチはBezier clipping法で抽出できる。   TVC('91) ；曲面(穴のあるtrimmed Ｂｅｚｉｅｒ曲面に適用可）のスキャンライン法に応用   CGI'93 ；ＮＰＲへの応用（輪郭と濃淡がＢezier曲線で指定されている）  EG93 曲面を含むラジオシテイに応用した例。  Bezier Clipping を用いた 2 次元画像の自由形状変形法 |
Bezier Clipping関連の著者らの論文
|
|
|
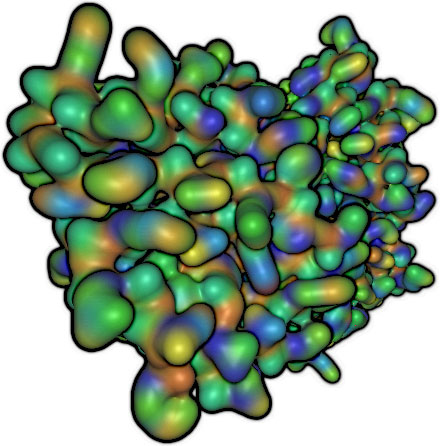
メタボールは、Blinnがblobと呼んで最初に発表し、独立に大阪大学がmetaballと称し
た。 西田らは、メタボールの表示を数倍早くする方法をＥＵＲＯＧＲＡＰＨＩＣＳで発表した。メタボールの密度関数は6次の多項式で表現できるので（ここでは6 次式）、多項式の解 を算出するのにBezier Clippingが有効である。 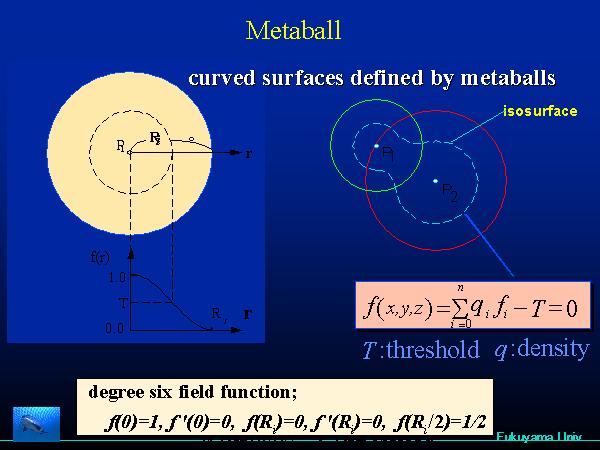 左の図のように、メタボールは中心をピークとした密度分布で与えられている。メタボースが接近するとこれらの密度は加算される。指定した閾値の面を抽出す ることで、表面を求める。この方法は陰関数表現された面と言える。 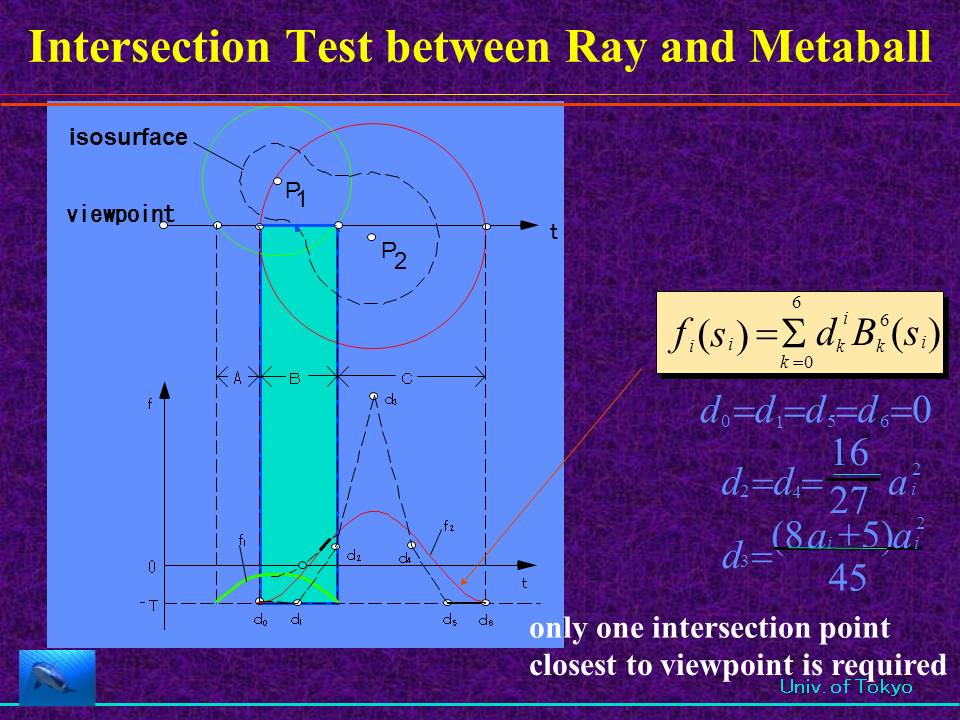 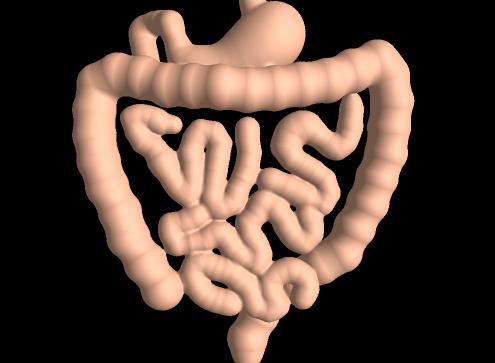  EUROGRAPHICS'94； 右の図は楕円体のメタボールを組合わせてものである。   SIGGRAPH'94： シャチは800個以上のメタボールで構成している。ボールなので泳ぎに合わせて変形するのは容易である。    ShapeModeling'99： 日本人女性の標準体系形のデータを入手し、その形状にフィットしたメタボールを生成して人体を作成した。加えて、そ れに洋服 を着せるシミュレーーションを行った。     最近、ＧＰＵを使い高速化（ほぼリアルタイム）した方法をＥＵＲＯＧＲＡＰＨＩＣＳで発表した（金森が筆頭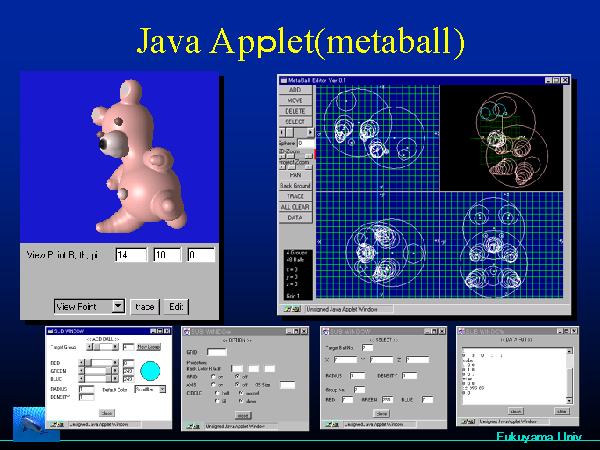）   Ｊava アプレットを用いて、メタボールの会話的に入力し、それを表示する。 他にも、多項式の解、曲線同志の交差判定、曲線と任意の点との最短距離の抽出などのアプレットを作成した。 |
 西田らのメタボールの表示例   メタボールとは限らないが、粒子として表現する描画法の計算例  謝辞； この研究に関し、元指導教授の中前教授に加え、共同研究者の金田先生、岩崎先生、金森先生に感謝する。 |
|
|
 西田の論文（1990）を読んで、レイトレーシング法を商品化したものであ
る。これはＮＫエクサ社が実用化。
  |
|
| |
|
Bezier Clippingとは 
Ｂeｚｉｅｒ
Clippingによる曲面のレイトレーシング 
