5.8 バンプマッピング
みかんの肌、道路等は細かな凹凸があり、これがその材質固有の光沢を表現します。これは、表面の凹凸により、光の反射方向が変化され明暗模様が現れるからです。物体の表面の無数に近い凹凸を疑似的に表現する方法がバンプマッピング(bump mapping)です。この方法はブリン(Blinn)により最初に開発されました。これはテクスチャーマッピングがスカラマッピングであるのに対して、物体表面の法線ベクトルをマッピングし、それに光を当ててその点の輝度を計算するものです。法線ベクトルとしては乱数、連続関数、または濃淡画像の濃度値を微分したもの等を利用します。説明を簡単にするため2次元図形を用いて説明しましょう。実際の凹凸(すなわち、基準面からの変位)が図5.31とします。
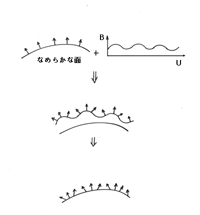
図5.31： バンプマッピング(法線ベクトルの摂動)
凹凸を構成する微小平面の法線ベクトルは図5.31(b)(図中の矢印)のようになります。これらの法線ベクトルを滑らかな曲面上にマッピングします。これは、曲面の概形を与える滑らかな曲面(smooth surface)に、しわ関数(wrinkle function)をマッピングすることです。曲面上の座標をパラメータ座標(u, v)とする。また、滑らかな曲面上の点P[x(u, v),y(u, v),z(u ,v)]での面のu方向の接線、およびv方向の接線ベクトルは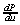
,
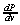であるから、法線ベクトルNは次式で表わされます。
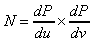(5.18)
また、バンプデータをBとし、曲面上の点(u, v)に対応するバンプデータの座標を(s, t)とします。新しい法線ベクトルＮ'は
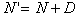(5.19)
なお、
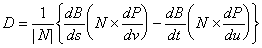(5.20)
です（図5.32参照）。
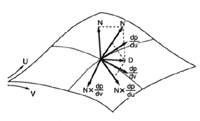
図5.32： 新しい法線ベクトルの算出
ここで、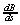
,
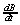はバンプデータ中の(s, t)に相当する要素とそれに隣接する要素との差として求められます。 物体表面の不規則な凹凸を生成する技法として、フラクタル理論を用いる方法も開発されています。
図5.33： バンプマッピングの表示例
図5.33はティーポットにバンプマッピングしたものです。
図5.34: 濡れた路面のバンプマッピングの表示例
図5.34は濡れた路面をバンプマッピングで表現した例を示します。また、法線ベクトルを摂動させるのなく、凹凸の変位そのものをマッピングするディスプレイスメントマッピングという技法も開発されています。
前のページへ