   |
   |
物体を照射する光は直射光と間接光に分けられます。直射光はさらに (a) 平行光線(太陽光)、 (b) 点光源(電灯、スポットライト)、 (c) 大きさをもつ光源(蛍光灯、間接照明)、 に分けられる。大きさをもった光源として線光源、面光源などがあります。被照面の反射光は、拡散反射と鏡面反射成分からなり、ほとんどの物体は両成分を含んでいます。 間接光は環境光とも呼ばれ、一般には画面全体に一定の明るさを与えます。環境光(ambient light)による反射光Iの強さは次式によって与えられます。
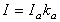 (5.1) (5.1)
ここで、 拡散光は、入射角に関係なくいずれの方向にも同じ強さで反射します。これは、紙等のように表面がざらざらしたものにみられ、以下に光源の種類に応じた計算法を説明します。
平行光線の場合、反射光の強さは入射角の余弦に比例します。この法則をランバート(Lambert)の余弦則といいます。平面を平行光線で照射した場合、面上のどの点でも反射光の強さは一定です。図5.3に示すように、入射光の強さを
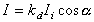 (5.2) (5.2)
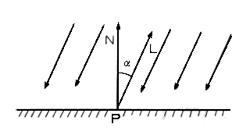
図5.3: 平行光線による面の輝度
ここで、αは入射角すなわち面の単位法線ベクトルNと光線の方向を示す単位ベクトルLとのなす角であり、 それでは、平行光線・ランバートの余弦則を用いた凸多面体のシェーディングモデルの表示をJavaで実際に体験してみましょう。
点光源の場合には、距離の逆2乗則およびランバートの余弦則に従います。図5.4に示すように、光源Qの光度を
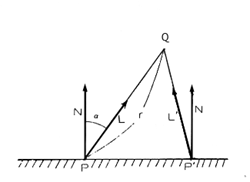
図5.4: 点光源による面の輝度 点Pでの反射光の強さは、
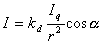 (5.3) (5.3)
となる。
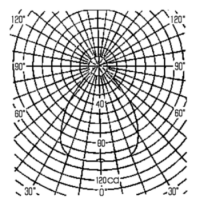
この配光特性は灯軸からの角度θの関数

図5.6:配光特性を持つ点光源に照射された日本間の表示例 図5.6は、どのような配光をもつ点光源が適当かを検討するためのCG画像の例 (右上に配光が示されています)です。 大きさをもつ光源の代表的なものは面光源です。この場合、ある点での反射光の強さIは、m多角形の光源を考え、光源の単位面積当りの光度をLとすると、ある点での反射光の強さは、次式の境界積分法によって求まります(図5.7参照)。
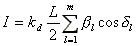 (5.4) (5.4)
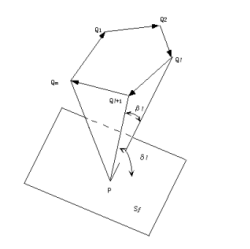
左図では、

左図は面光源で照射した室内の計算例です。 よく磨かれた壷が照射された場合、鏡面反射により、表面の一部にハイライトを生じます。鏡面反射は、入射と反射角が等しい方向に光が反射される。 完全鏡面反射でないものは、正反射方向の近傍にも反射されます。なお、曲面のハイライトは工業デザインに特に重要です。
簡易法として、視線と正反射方向のずれ角γによる鏡面反射成分の減少の割合を
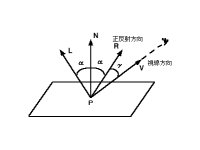
図5.9: フォングの反射モデル 鏡面反射光の強さをIとすると、
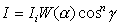 (5.5) (5.5)
ここで、
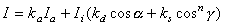 (5.6) (5.6)

左図はnおよび反射率を変化させた場合の比較です(上の段は
上記のγだけでなく、より物理法則に基づくため、反射面と視線との角度、表面の粗さによる鏡面反射成分の分布特性を考慮したものであるが、計算時間がかかる。 (c) クック・トランス(Cook-Torrance)のモデル 精密なモデルとして、反射率は波長および入射角に依存することも考慮し、反射率はフレネル(Fresnel)の式を用いた。特に金属の表示に適しているが、より一層計算時間は大きくなる。面は微細な面の集合と考え、面の法線ベクトルの方向を中心にある分布をしてるものとする。光の光線ベクトルをL、視線をVとし、これらの2等分ベクトルをHとする(図5.11参照)。ここでHは次式である。
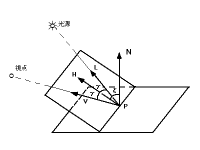
図5.11: クック・トランス(Cook-Torrance)のモデル
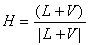 (5.7) (5.7)
さらにHとNとの角を
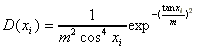 (5.8) (5.8)
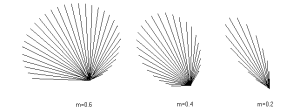
図5.12にmが変化した場合の分布関数(入射角30度の時)を示します。

上図に金属の反射の違いを示します。(左上から、金,銀,銅、右下から鉄,アルミだじょー)。
|
 前のページへ 前のページへ
| 次のページへ
|