波は、波の峰と谷で水粒子の運動が異なるため、波は正弦波からずれてきて、波の峰が尖り、谷が平らになる傾向がある(図1、2参照)。
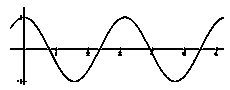 図1 正弦波
図1 正弦波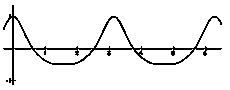 図2 ストークス波
図2 ストークス波
水の波の波動理論では、通常、水は非圧縮性で非粘性、波動運動は非回転とし、周期Tと波高Hの定形な周期波として取り扱われる。一般に波の運動は水表面近くで著しく、深部では漸次消滅する。また一つの水粒子に注目すると、それは波の一周期の間に円または楕円のような閉軌道を描くものとみてよい場合が多い。そして、波動は水面付近に限られ、水底付近は静止している。このような、波動を表面波という。一般に、波長が水深の半分以上であれば表面波と考えることができる。ここでは表面波を扱う。
波は、波の峰と谷で水粒子の運動が異なるため、波は正弦波からずれてきて、波の峰が尖り、谷が平らになる傾向がある(図1、2参照)。
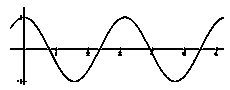 図1 正弦波
図1 正弦波
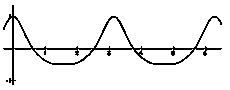 図2 ストークス波
図2 ストークス波
ストークスは、この波の解析式を、次のようなFourier級数形式で与えられるとした。この波をストークス波と呼び、以下の式で与えられる。
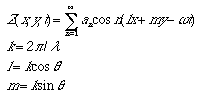
Z(x,y,t):波高
an:各高調波成分の振幅
l:x方向のラジアン波数
m:y方向のラジアン波数
w(omega):角振動数
t:時間
theta:波の進行方向のx軸に対する角度 [度]
lambda:波長
ここで、ストークスは、各高調波成分の振幅において、第4高調波成分までを、以下の式で与えられるとした。
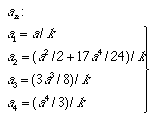
このストークス波は、比較的単純な計算でリアリティーのある波を生成することができるので、Nelson Maxにより、コンピュータグラフィックスによる水面の表示に用いられた。
[アプレットの使用方法]
本アプレットでは、以上の式において、スクロールバーを用いて以下の項目について変更できる。
(1)各高調波成分の波長(lambda)[m]
変更可能な範囲は0.〜50.[m]
(2)各高調波のx軸に対する進行方向(theta)[度]
変更可能な範囲は−180.〜180.[度]
(3)各高調波の角振動数(omega)[度/sec]
変更可能な範囲は0.〜360.[度/sec]
(4)波の振幅(上式においてa)(amplitude)[m]
変更可能な範囲は0.〜1.[m]
Resetボタンをクリックすると、各パラメータ、視点が、初期化される。
